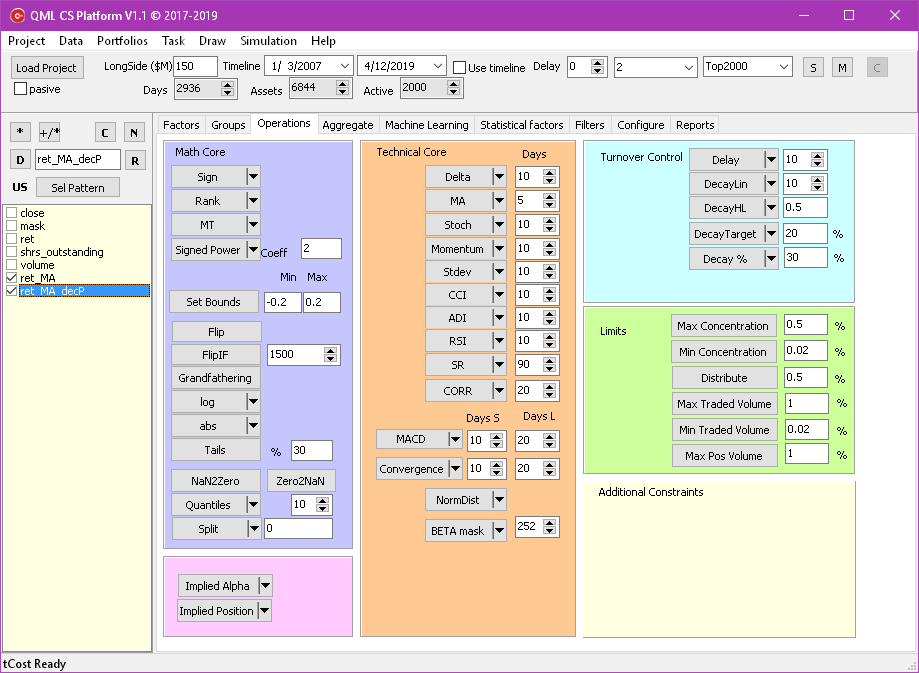
The philosophy behind this framework is “an algebra of alphas”. Mathematically, an alpha is a matrix with two dimensions: time and universe of assets. One, two or more such matrices can interact via operations of various kinds, resulting in one or more such matrices.
Case 1. 5-Day Reversion
For instance, if we believe that 5-day moving average of returns is a reversion signal, we apply an operation that will compute a new matrix by processing the return matrix, taking for each column the sum of the last five entries with a negative sign. Then, we believe that the reversion signals are stronger if the information is fresh. So we shall backtest in delay 0 mode. (Market DeMean and Normalize will allow the performance measurements to be evaluate correctly).
Plot the cumulative PnL and notice:
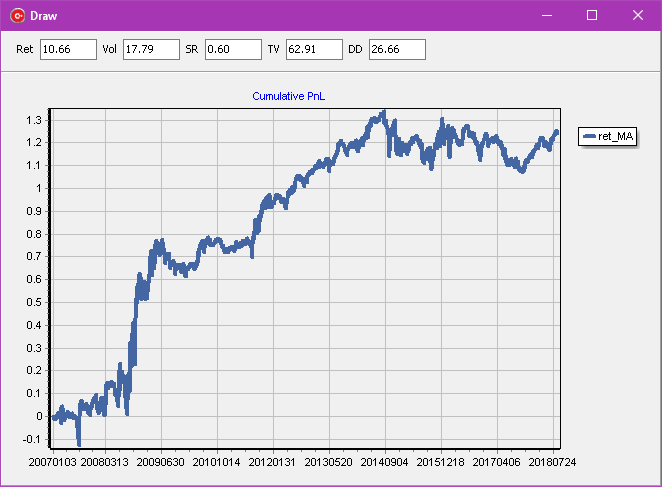
That is a good start, but we need to improve performance (Sharpe ratio) and to reduce trading costs (decrease the turnover).
First, let us try subindustry neutralization. That will lead to:
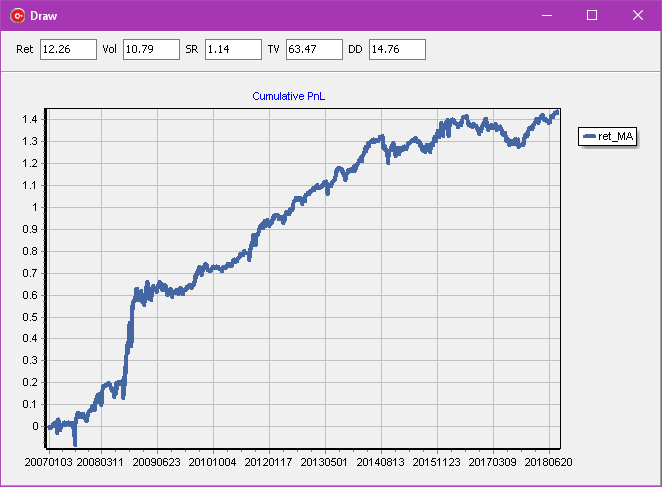
We proceed with Factor Neutralization (all 20-and standardize again):
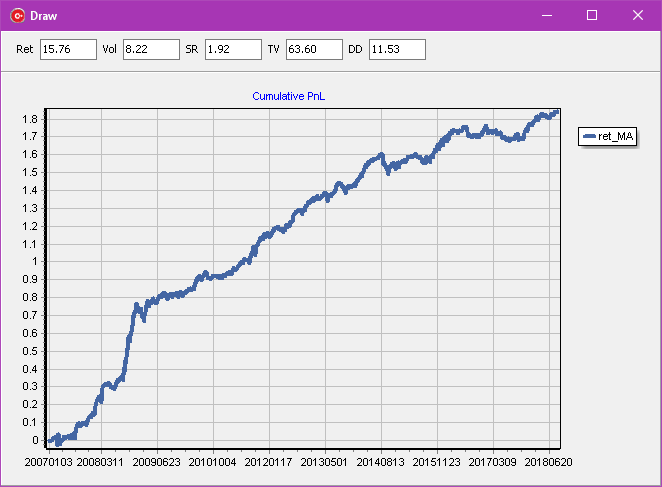
Now, we want to decrease the speed of trading, as it can be costly. We apply a decay operation of this signal to 30% turnover:
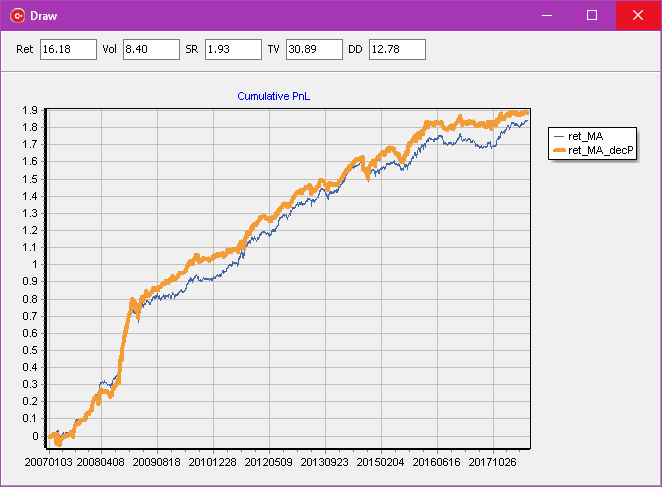
Why is the orange signal preferred to the blue one? Because if we apply 2bps trading cost, the picture changes significantly:
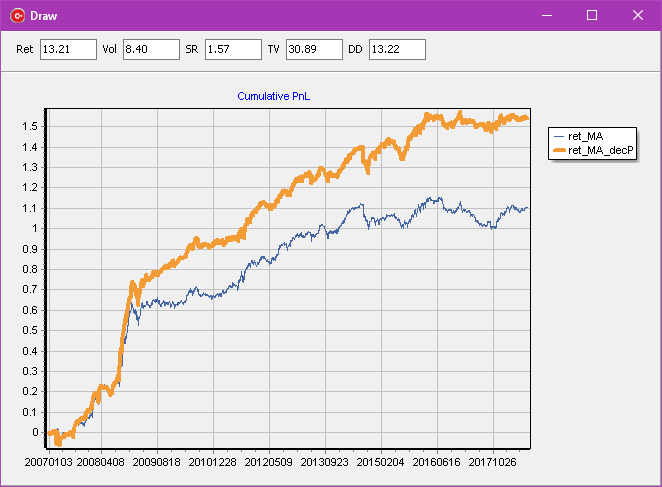
This kind of research can be augmented with many operations: