Biclustering Algorithms are related to association rules and recommendation systems. They are also solving the problem of enumerating all maximal complete bipartite subgraphs of a bipartite graph.
The problem is to detect in a relationship involving two kinds of entities what are the maximal connections.
Example. A number of customers would pick similar items during their shopping trips at one particular store. The manager of the store realizes that rearranging the items on the shelves could reduce the time customers spend in the store and that leads to better utilization of the store space and of better usage of customers’ time.
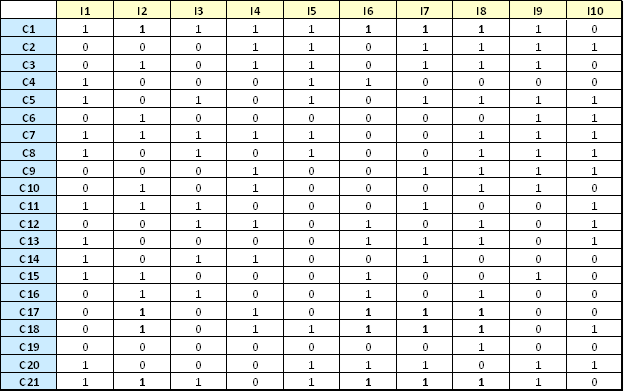
In the example below, C1-C21 are customers and I1-I10 are items. The intersection of row C6 and column I2 equals 1, and that means that customer C6 usually buys item I2. The entry (C4,I2)=0 means that customer C4 does not buy item I2 frequently.
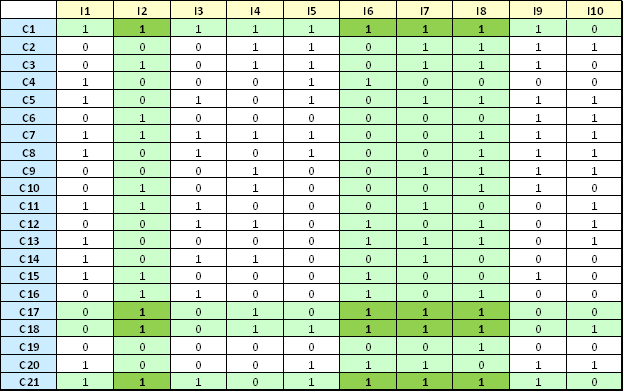
The application of the biclustering algorithm to this problem will generate 149 maximal connections between clients and items. Here, we illustrate (in dark green) one which is interesting as it connects a relatively high number of clients (C1, C17, C18 and C21) with a high number of items (I2, I6, I7 and I8).
High Performance
The implementation of this algorithm uses developments of MICA, augmented with bitwise operations and parallel execution.
The full description of the algorithm in given in the paper:
Consensus Algorithms for the Generation of All Maximal Bicliques
Download an educational software for MICA
Download the file containing the input matrix for the above example:
Run the program, open the input file you just downloaded, run the program (and inspect the output). Among the results you should find this maximal biclique:
1,17,18,21 : 2,6,7,8
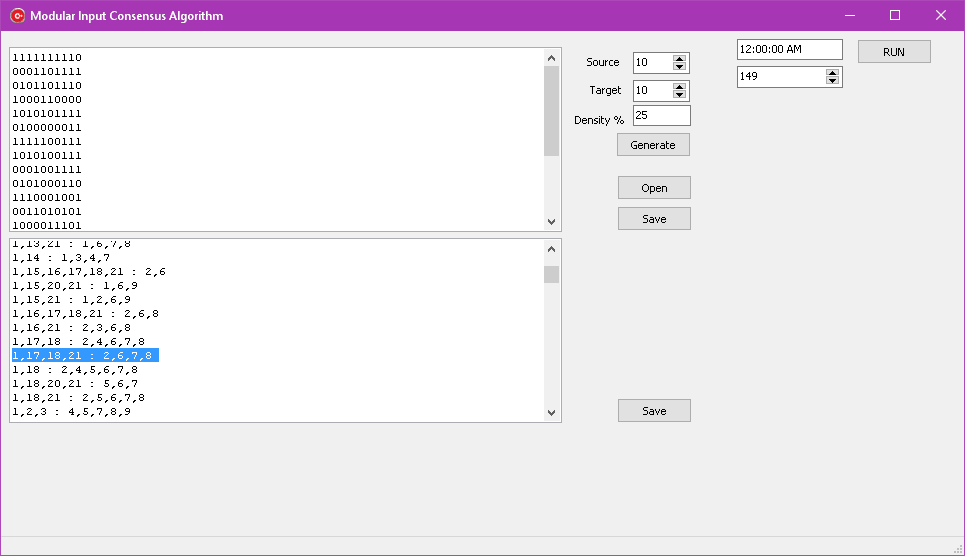
Vertex labels start with 1.
The vertices from the left of the colon separator (“:”) belong to the left side of the graph (Clients in the example above) and the vertices from the right (Items)
C1, C17, C18 and C21 are connected to I2, I6, I7 and I8, the one depicted in the second table of this page.